Abstract
MDFourier is an open source software solution created to compare audio signatures and generate a series of graphs that show how they differ. The software consists of two separate programs, one that produces the signal for recording from the console and the other that analyses and displays the audio comparisons.
The information gathered from the comparison results can be used in a variety of ways: to identify how audio signatures vary between systems, to detect if the audio signals are modified by audio equipment, to find if modifications resulted in audible changes, to help tune emulators, FPGA implementations or mods, etc.
This document serves as an introduction, a manual and a description of the methods used and how they work. Its intent is to guide new users in making simple comparisons while still providing advanced users with information to perform a more detailed analysis of audio signatures.
MDFourier is a free and open source software suite for analyzing and comparing audio signatures.
It can be used to identify the differences between two audio recordings. For instance, a Sega Genesis Model 1 VA3 and a Sega Genesis Model 2 VA 1.8 can be compared in order to verify how they differ across the human hearing frequency spectrum, using objective and repeatable results.
The process is not limited to one specific system, and the software can be configured to make comparisons for other platforms with the addition of new profile files.1 At the moment, profiles for Mega Drive/Genesis, Mega/Sega CD, PC Engine/Turbografx-16 and its CD-ROM addons are functional–with more to follow.
The intention is not to disparage any particular system, but to promote a better understanding of audio variations, while allowing those who wish to modify their consoles the ability to accurately identify the differences.
A secondary, but not less important goal is to create a community driven catalog of audio signatures from these systems and the variations between consoles for archival and preservation purposes.
It is my personal opinion that it would be useful to have configurations tuned to replicate the audio signatures of original retail hardware variations in emulators and Field-programmable gate array (FPGA) implementations. This, however, does not mean there in not room for improvement. Reducing noise while keeping the reference sound signature is one such scenario.
Although powerful industrial solutions for this kind of analysis must exist, they do not seem to have reached the enthusiast community. I’m not aware of any other similar effort to create public software analysis tools that are aimed at vintage console hardware.
It must be noted that there have been detailed comparisons, made in particular for the MegaDrive/Sega Genesis.2
There is also some interesting information that is derived from the analysis, and which is displayed as part of the output:
MDFourier and this documentation are a work in progress. Although I tried to adhere to best practices, my experience in digital signal processing was almost non-existent before this project.
Please contact me if you have corrections, improvements, suggestions or comments. These are encouraged and welcome. Contact information is available in appendix Q.
This project was born out of my curiosity to compare the audio signatures of different revisions of the Mega Drive/Genesis, and verify them with a tool assisted analysis. Due to my interest in game preservation it naturally evolved into its current form, and will hopefully continue to grow.
This chapter is an introduction to the audio concepts that will be used throughout the document, such as: frequency, amplitude, sample rate, decibel, etc. Hopefully it can provide a simplified–but functional–perspective to those unfamiliar with audio and its digital representations.
Sound is a series of vibrations that travel through a medium. In our case this medium is typically air, but it can be water or even a solid. These vibrations are waves of pressure and–as any other wave–they have characteristics that we can measure in order to classify and understand them.
We use the term frequency to refer to a repeating event–how frequent it is. In this case it means how many times the wave we are measuring repeats in a second. We measure this in cycles per second, and use a unit named Hertz (Hz).
As you can imagine these vibrations in the air can have a wide range of frequencies, but we can’t hear all of them due to biological limitations. The range that humans can typically perceive is called the human hearing spectrum. A spectrum refers to a continuous range of frequencies, and in this case it is defined to start at 20Hz and end at 20000Hz–we commonly use the term 20kiloHertz, since kHz refers to multiples of 1000Hz.1 These numbers are of course an average, and every one of us has a different hearing spectrum that also changes as we age.
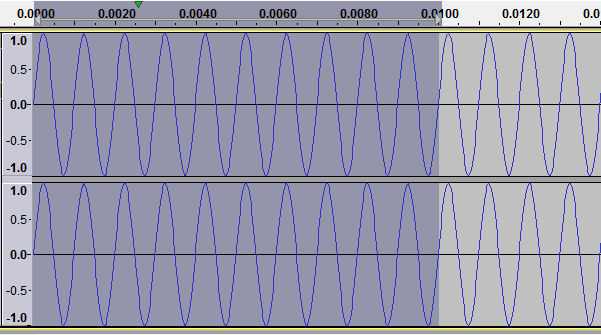
In Figure 2.1 we can see a frequency of 1kHz in an audio editor. We can tell it is 1000 cycles per second since the darker selection spans for 0.01 seconds, and it has 10 complete wave cycles in it.
We perceive frequency variations as pitch differences: lower frequencies are what we call bass and higher frequencies are treble–corresponding to lower and higher pitched tones.
The other wave characteristic we use to measure sound is called amplitude. This is how powerful the wave is when compared to the rest of the signal that is being analyzed.
Figure 2.2 shows a 1kHz signal that starts at the highest amplitude in an audio editor and goes down to zero. This is a typical fade out, but done in a very short period in order to show both frequency and amplitude in the same image.
We perceive this amplitude as volume, and the terms are directly related. In general, the higher the amplitude of a sound pressure wave, the higher the volume we perceive. But since a sound with the same amplitude but at another frequency can be perceived as a different volume by the human ear, the terms don’t mean the same thing. Since the software can only use amplitude for its calculations, we’ll use that term throughout the whole document.
The unit used to measure amplitude in sound pressure waves is called decibel (dB). These use a logarithmic scale, which means that in it each subsequent number is a multiple of a base quantity, instead of a sequence of incremental values by a unit as in a linear scale.
We use this scale since it closely models the way we perceive sound, and also because sound amplitudes have a very wide range. For instance, the use of a logarithmic scale allows us to simultaneously compare the variations of the ambient sound levels from a library against those from a rock concert–even if they are in opposite sides of the human hearing spectrum. You might be familiar with this concept from other logarithmic scales, like the Richter scale used to measure earthquake strength.
Using the scale might be confusing at first, so we’ll use an example in order to show how the values behave. Imagine we have two sources that are individually measured as having a sound pressure level of 9dB. If both sources produce sound at the same time, we will measure a combined sound pressure level of 12dB instead of the 18dB that one might have expected when using a linear scale.
This doesn’t mean you’ll need to use logarithm algebra when dealing with this document–or with sound in general. In practical terms whenever you see a 3dB difference in sound amplitude, it means that you’ll perceive twice the volume.
This scale starts at 0dB which is the inferior limit of human hearing, and goes up to 194dB; where the sound barrier is broken and it becomes a shock wave, at least in the earth’s atmosphere. The following table has some common values:2
| dBA | Source |
| 0 | healthy hearing threshold |
| 10 | a pin dropping |
| 20 | rustling leaves |
| 30 | whisper |
| 40 | babbling brook |
| 50 | refrigerator |
| 60 | conversational speech |
| 70 | vacuum cleaner at 1 meter |
| 80 | alarm clock |
| 85 | passing diesel truck |
| 90 | squeeze toy |
| 95 | inside subway car |
| 100 | handheld drill |
| 110 | rock band |
| 115 | emergency vehicle siren |
| 120 | thunderclap |
| 125 | balloon popping |
| 130 | peak stadium crowd noise |
| 140 | jet engine at takeoff |
| 145 | firecracker |
| 150 | fighter jet launch |
| 180 | rocket launch |
| 194 | sound waves become shock waves |
In this section, we will be describing how the audio is encoded in a format called Pulse-code modulation (PCM). It is what a Waveform Audio File Format (WAV ) file uses internally, and the format MDFourier can use for analysis.3
Sound is a continuous signal that varies in time. This means that if you could zoom into it at the smallest fraction of time imaginable, you’d also have a tiny bit of sound happening during that lapse.
Unfortunately computers don’t have the unlimited storage that would be able to replicate a continuous signal–and they also have speed limitations. In order to represent sound in the digital domain we use a process called sampling.
Sampling involves measuring the amplitude of the sound pressure wave at regular cycles–at a frequency–and assigning a value to each one of this measurements. The frequency at which we take each of these samples from the continuous audio signal is called the sampling rate.
The sample rate defines the frequencies from the signal that we will be able to represent in the digital domain–as the sampling rate is increased, so does the frequency range that can be portrayed by this digital representation of the signal.
If we want to represent a certain frequency range reliably, we must choose a sample rate that is twice as big as the highest frequency value in the desired spectrum. This principle is called Nyquist–Shannon sampling theorem, and it requires a band limited signal in order to work. For a signal to be band limited it must not contain frequencies higher than those that we wish to represent. In order to eliminate frequencies higher than a certain value, we use a low pass filer before digitizing the signal.
Since we want to cover the whole human hearing range–which goes from 20Hz to 20kHz–we must choose a sample rate of at least 40kHz. This is the reason for the most common sample rates in digital audio to be 44.1kHz and 48kHz–which are the ones supported by the Analysis Software in MDFourier.4
When we create a digital representation of the amplitude value for each sample, we must define a bit depth. In other words we must choose the amount of bits–the minimal piece of data in our current computing systems–that will be used to store each number.
A common choice is to use 16 bits for each measurement. With this we can represent each sample with values that range from -32,768(-1 × 215) up to 32,767 (215 - 1). We’ll look into what this implies during the next section.
Among other things, this decision affects the resulting file size of the audio recording. If we use a 24 bit depth, files will be 150% bigger than their 16 bit counterpart if no compression method is used.
When we were measuring amplitudes before, we used the dB. In that scenario we were analyzing amplitudes that start at the minimum amplitude our human ears can detect and assigned a value of 0dB to that level. Values can theoretically go up without limits–aside from that pesky sound barrier we mentioned before when using air as a transmission medium.
However when dealing with digital values that have a defined bit depth, our limit is fixed from the other side–the biggest amplitude we can represent with a limited number of bits. This number is easily calculated, for n bits we get 2n possible values.
Because of this, when using digital files we use a variation of the decibel named decibels relative to full scale (dBFS). The highest possible amplitude starts at 0dBFS and values go down into negative numbers, until they reach the lowest amplitude that can be represented by the selected bit depth. When using a bit depth of 16–as used in Compact Discs and by the Analysis Software in MDFourier–the minimum amplitude that can be represented is -96dBFS.
This is commonly referred to as the dynamic range, and it tells us how far apart the minimum and maximum amplitudes that can be represented in a audio recording are. For example, if we have a dynamic range of 96dB, we can represent the relative amplitudes of thunderclap and rustling leaves within the same recording; but we could have no lower or higher amplitudes since they’d exceed the range.
Some common formats use 24 bit audio, which has a wider dynamic range that can cover 144dB. One must think that more is always better, but there are valid reasons that explain why this format is not widespread in consumer products.
Current digital audio converter technology can only deal with around 120dB, which makes a big part of the advantage go to waste. And secondly, we rarely have a need for such a wide range in our typical recordings. With certainty for the cases that will be analyzed by MDFourier the 96dB range from 16 bit audio is more than enough.
For studio and mixing applications 24 bit audio is a huge advantage, since the dynamic range available with the 16 bit variant can be easily surpassed when mixing signals from similar amplitudes and end up causing undesirable saturation of the resulting signal.
The software components that allow MDFourier to make comparisons for a particular platform are:
The whole process is shown in Figure 3.1, including the main hardware components.
MDFourier takes two signals, the first one is designated as the Reference file. The second one is the file under scrutiny, and is referred to as Comparison file.
The first step is loading the Tone Generator to the desired system that will be analyzed. The process for this varies with each platform: from placing the software in a flash cart, burning a CD-ROM or using a custom loader.
The next step is preparing an audio capture device and a computer, in order to record an audio file.1 Once the audio card is ready, and the cables are hooked up from the system to the audio inputs, the recording process is started from the computer and the Tone Generator should be activated from the system under analysis.
After a short lapse, usually around one minute, the Tone Generator will display a message indicating that the recording process can be stopped. When at least two files are available, one to be used as reference–which can be one of the files provided–and one to be used as comparison file; a comparison can be made with the Analysis Software from the computer.2
The Reference file is used as a control. This means that its characteristics are considered the true values to be expected and against which the Comparison file will be evaluated. In consequence, all results are relative between the signals.
Having these files, the software analyzes and compares their audio characteristics and generates graphs that visually show how they differ.
These files are audio recordings from the desired hardware, preferably captured with a flat frequency audio capture card and produced by a the Tone Generator that runs on the target platform.3 This Tone Generator is specifically crafted for the particular hardware capabilities and frequency range of the target. Whenever possible, the Tone Generator will be included in the 240p Test Suite for the platform to be analyzed.4
Although the Analysis Software is command line based–in order to be multi-platform and offer the tool on every operating system that has an ANSI C99 compiler–a Graphical User Interface (GUI) front end for Microsoft Windows is provided for simplicity and accessibility. Full Source code can be downloaded from github.5
MDFourier takes both files and auto detects the starting and ending points of the recording. These points are identified by a series of 8820Hz pulses in the current Mega Drive/Genesis implementation. This process allows the calculation of the frame rate at which the system was running,6 so that the recording can be precisely trimmed into the segments that are defined through the configuration file for further analysis.7
This process guarantees that the reference and comparison files are logically aligned, and that each note–or segment–is compared to its corresponding one. The results have no overlap, and no audio editing or trimming skills are required from the user. The current pulse detection accuracy is around 1 ∕ 4 of a millisecond.
After alignment is complete, the software reports the starting and end points of both signals, in seconds and bytes.
A process called Discrete Fourier Transform (DFT) is used in order to analyze and compare the amplitudes from each of the frequencies and harmonics–the spectrum–that compose the audio signal.8
In order to compare the frequencies and amplitudes of each file against each other, a reference point must be set. This is achieved via a relative normalization based on the maximum amplitude of the Reference file.9 A local maximum search is done at the same frame in the Comparison signal, and that amplitude is then used to normalize both files.
This is done in the frequency domain, in order to reduce amplitude imprecision when comparing recordings with different frame rates.10 The software does have the option to do this in the time domain, but quantization and amplitude imprecision is to be expected if used.11
After normalization is finished, the frequencies of each block are sorted out by amplitude, from highest to lowest.12 MDFourier can be configured to compare a range of these frequencies–by default 2000 of them are compared for each block defined in the mfn configuration file.13 I’ve found such number to be more than enough, and usually the minimum significant amplitude limits this parameter to an even lower number.14 In case a different comparison of frequencies is needed, the amount can be increased or decreased via the command line or extra commands option.15
It can be helpful to listen to the results of these parameters and filters, in order to evaluate if things like limiting the test to 2000 frequencies is sufficient data for the analysis. For this and other purposes I made an extra tool named MDWave, which creates segmented audio files as internally processed by MDFourier, including all the processing filters and amplitude limits.16
After comparing these frequencies between both files, the corresponding matches are found and the amplitude differences are plotted to a graph. Please refer to chapter 4 for an explanation of the various graphs created by this program.
If you are interested in learning what the Fourier Transform does and how its "magic" works, there are several resources online. Here are a few of them:
Although the whole frequency spectrum can be compared, there is little practical use in doing so–due to execution time and extra noise from low amplitude harmonics. As a result, rule of thumb defaults are set in order to minimize these issues.
One of these values is a minimum amplitude at which to stop comparing the fundamental frequencies that are found after decomposing the signal with the Fourier Transform. This is the minimal significant amplitude and it is the cutoff at which comparisons made by the software are stopped.
Currently MDFourier can recognize three scenarios to define the minimal significant amplitude to compare the signals, and the three are derived from the first silence block in the file.
The first scenario is the electrical grid frequency noise, which is searched for at either 60Hz for NTSC or 50Hz for PAL. This is automatically selected from the previously calculated frame rate, if available.
The second one is refresh rate noise, again derived from the frame rate for each specific console. In NTSC it is around 15kHz.
If neither is found–which would be surprising for a file generated by recording from a vintage console via analogue means–the frequency with the highest amplitude within the silence block is used.
Finally, in case none of the previous scenarios is met, or if those values are lower than -60dBFS, a default level of -60dBFS is used.17
The main output of the program is a set of different graphs that vary in quantity based on the definitions made in the mfn file,1 and the selected options.2
The graph files are saved under the folder MDFourier and a sub-folder named after the input WAV file names. They are stored in Portable Network Graphic (PNG) format. Currently 1600x800 graphs are used, although this can be changed via options.
For the current document 800x400 graphs were used in order to fit within a PDF or HTML presentation. The output graphs that are created by the software are listed and described in appendix B.1.4.
In our examples for the Mega Drive/Genesis, there are three active blocks3 : FM, PSG and Noise. These will result in a graph of each type, plus a general one named ALL.
We’ll follow a series of results from different input files to MDFourier, starting with cases that have either none or a few differences and build on top of each one, so you can familiarize with what to expect as output.
The first scenario we’ll cover is the basic one, the same file against itself. Let’s keep in mind that MDFourier is designed to show the relative differences between two audio files.
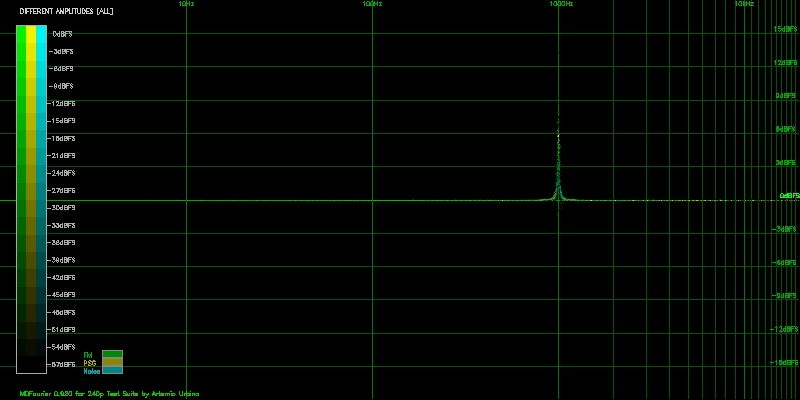
So, what is the expected result of comparing a file to itself? No differences at all. An empty graph file as shown in Figure 4.1.
Of course all of the Differences and Missing graphs will only have the grid and reference bars, with no plotted information since both input files are identical.
All graphs use the horizontal axis for frequency. Values start from 1Hz on the left and end at 20kHz on the right, which covers the human hearing spectrum.4
For Difference graphs the vertical axis is the amplitude in dBFS, and a central axis for 0dBFS. Values rise to 18dBFS towards the top and fall to -18dBFS on the lower part of the graph.
There will be two sets of Spectrograms, one for the Reference file and one for the Comparison file, with one graph for each defined type plus the general one.
The Amplitude of each of the fundamental sine waves that compose the original signal is represented by vertical lines that reach from the bottom to the point that corresponds to the amplitude in dBFS. The line is also colored to represent that amplitude with the scale on the left showing the equivalence.
Three colors–as defined from the mfn file5 –are used to plot the graph, with each one of them plotting the frequencies from each corresponding type from the WAV file.
The top of the graph corresponds to the maximum possible amplitude, which is 0dBFS. The bottom of the graph corresponds to the minimum significant amplitude, as described in section 3.5.
As expected, both sets of spectrograms are identical in this case, since we used the same file compared against itself.
This is another control case. What should we expect to see if we record two consecutive audio files from the same console using the same sound card?
As you can see, we have basically a flat line around zero. This means that there were no meaningful differences found.
But wait, there are differences. Why is that? Due to many reasons: analogue recordings are not always identical, but they should be lower than this. There are also variations from the analogue part of console itself, and probably from the internal states and clocks from the digital side of the process.
But in this particular case they are fluctuations present in the FM signal–shown in green here–as demonstrated by comparing other kind of digital audio recordings with the Analysis Software.6
We now know that there can be certain amount of fuzziness, or variation, around each graph when comparing certain kind of signals due to this subtle performance nuances. It is a normal situation that is to be expected, and a baseline for further results.
Until now we haven’t discussed the small bars at the lower left quadrant of the graphs. These represent the percentage of matches that were made. In this case we get all above 99.8% as shown in Figure 4.4. This serves as a quick guide on how relevant the plotted differences are when comparing both signals. The numbers to the right are the amount of values that were compared.7
For demonstration purposes, the same Reference file was modified to add a 500Hz 6dBFS parametric equalization across all the signal. This is an artificially modified and controlled scenario in order to demonstrate what the graphs mean.
As expected all three types (FM, PSG and Noise) were affected and show a spike, exactly 6dBFS tall and centered around 500Hz.
It is interesting to contrast both spectrograms (figures 4.6 and 4.7), since the 500Hz spike is also shown there.
And the Missing Frequencies graphs are basically empty, since no relevant frequencies are missing from the Comparison file.
We will use the same Reference file, and compare it to a file modified by several digital filters that were inserted via an audio editor:
Figure 4.8 shows the general graph for the three types:
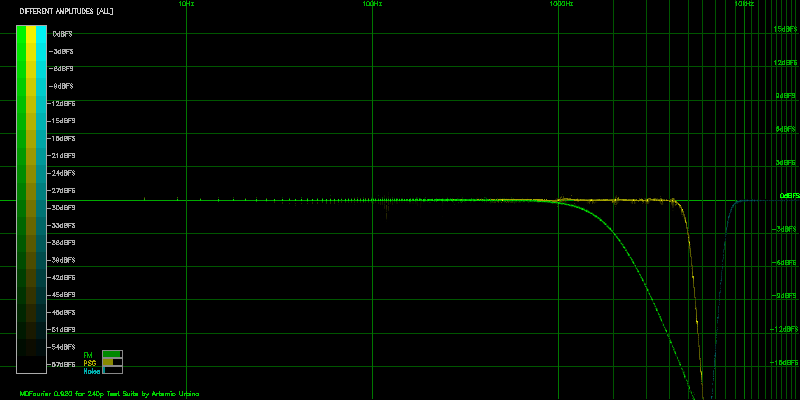
We can now see that the higher frequencies above 1kHz in the FM graph quickly fall down towards -∞dBFS, so the first low pass filter is there.
The second low pass filter for PSG is at 3kHz, and it is steeper.
But we can barely see what is going on with the Noise part of the graph. We can see that there is some black dots on top of the 0dBFS line.
In order to better see what is going on, we’ll change the Color Filter Function to "Bright" so we can have higher contrast against the background.10
With the new emphasis, we can now make out the curve that raises from -∞dBFS to 0dBFS, and it aligns with 8kHz.
We can still do better than that, by using the Average Graphs option.11
Here is the resulting graph for only the Noise section of the signal, with average enabled:
There are some other interesting graphs that result from this experiment. For example, the Missing graphs now show all the frequencies the low/high pass filters cutoff.
As shown in Figure 4.11, there is a curve in the spectrogram and only frequencies above 1kHz show up, slowly rising in amplitude. Many of these are not shown since they are below our defined minimum significant amplitude.
The same behavior can be observed in Figure 4.12. This is the PSG spectrogram, and it shows a different curve that starts at 4kHz.
As you might have noticed, a bar is also present in the Missing graph. But in this case it represents the percentage of unmatched frequencies, as shown in Figure 4.13.
And finally, Figure 4.14 shows the opposite kind of curve, the high pass filter that cuts off everything higher than 8kHz in the Noise section.
It is a good moment to emphasize that these are relative graphs. They show how different the Comparison signal is to the Reference signal. And so far we’ve compared the same signal to itself, although modified though very precise digital manipulations. An analog filter would look the same, but a bit fuzzier.
However, some interesting ideas arise. What would happen if we take this low/high pass filter signal and use it as Reference and the original one as Comparison?
Based on this, one could jump to the conclusion that everything will simply be inverted. After all, the original signal now rises to +∞dBFS at the same spots–and that makes complete sense–since those frequencies now have a higher amplitude.
Although the Differences graphs will indeed be inverted under these controlled conditions, the Missing graphs are different. Most of them are now empty:
This happens because although we cut a lot of frequencies with such steep low and high pass filters, all the frequency content from this modified signal is present in the original, but not the other way around as shown above.
We’ll now compare the same console using two different recordings, one made with the USB Lexicon Alpha and the other with a USB M-Track12 . Figure 4.17 shows the results:
There is some scatter, as it was to be expected from the results of Scenario 2.13 We can tell that the scatter is centered around the 0dBFS line, which means that even using different sound cards we discern differences between systems.14
Also, there was a slight difference in the detected frame rates. This happens since the sampling clock is not exactly the same in both audio cards.15 Here is the output text from the analysis that shows the detected frame rates:
At 48kHz both cards have very accurate sampling clocks with a minimal difference16 and MDFourier compensates for such issues.17 Differences can be more prominent when using 44.1kHz, but the software can still compensate for them without issues.
Here is the graph with the Average Graphs option turned on:
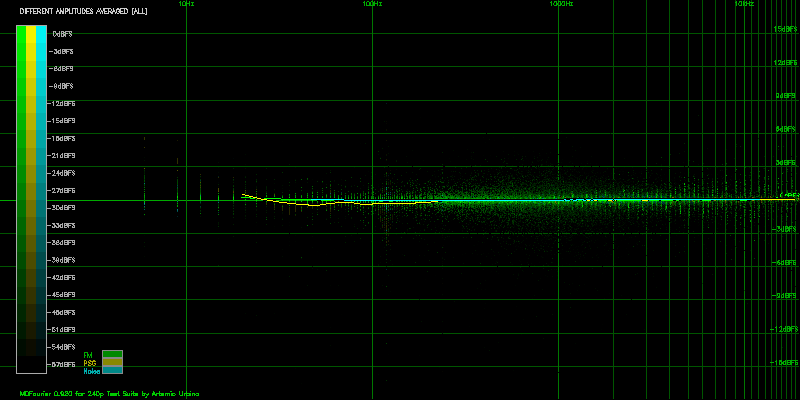
The results obtained are quite similar to the ones from Scenario 2, even to the point of getting almost the same percentages as shown in Figure 4.19. So as long as we are using a relatively flat frequency response audio card, we’ll be able to compare results from different systems even when using a variety of audio cards.
The audio file from Scenario 1 will be used as Reference and Comparison file, but this time encoded as MP3 and decompressed to WAV in order to use it with the software.18
If the files were identical, an empty graph would result as shown in Figure 4.1 from Scenario 1. However we get something slightly different:
We get everything centered around the 0dBFS–as it should be–which indicates the audio signatures are very similar. Variations are correspondent to what we found in Scenario 5 while we were comparing the same console with different audio cards. It must be noted that we used high quality compression for the test, and lower settings will provide different results. The reader is invited to experiment with the tools.
However in this case some more differences show up if we enable the Average Graphs option:
As it can be appreciated in the rightmost part of the graph, there is a low pass filter around 18kHz. These frequencies are at the border of acoustic human limits, and most adults won’t even be able to hear them. In part this is what MP3 compression relies on for reducing the required storage size of each audio file: cutting off frequencies that human beings are unlikely to hear. This is how the Fourier Transform helps to create smaller audio–and video–files.
Another side effect of using lossy compression19 –such as MP3–is the fuzzy cloud of amplitude differences present in the 500Hz to 8kHz range. We are highly tuned to this part of the spectrum, since most of the frequencies that typically compose the human voice reside here.20 This is most likely what some people perceive as lower quality audio when using these type of files.
Although impressive this is not good enough for our purpose, since we are trying to measure small differences between signals. This kind of noise would make it harder to identify the real source of the differences, specially with different encoding settings, audio cards and between consoles.
Another graph that shows the same differences is the Missing frequencies graph:
It can be appreciated that the missing frequencies were detected after the 18kHz line, aside from some harmonics below -45dBFS.
The following table lists all the hardware used to make the recordings for the graphs in this chapter. All systems had stock parts at the time of recording, no modifications and used original power supplies.1 .
The MDFourier ID value in the following table refers to the file name in the catalog, and will be used throught the text to identify the systems being compared.2
| Type | Model | Revision | FCCID | Serial | Region | Made in | MDFourier ID | Recorded from |
| Model 1 | HAA-2510 | VA1 | 89N61751 | Japan | Japan | A-MD1JJVA1 | Headphone Out | |
| Model 1 | 1601 | VA3 | FJ846EUSASEGA | 30W59853 | USA | Taiwan | A-MD1UTVA3 | Headphone Out |
| Model 1 | 1601 | VA3 | FJ846EUSASEGA | 30W59853 | USA | Taiwan | A-MD1UTVA3-AV | AV Out |
| Model 1 | 1601 | VA6 | FJ8USASEGA | B10120356 | USA | Japan | A-MD1UJVA6 | Headphone Out |
| Model 1 | 1601 | VA6 | FJ8USASEGA | 59006160 | USA | Taiwan | A-MD1UTVA6-1 | Headphone Out |
| Model 1 | 1601 | VA6 | FJ8USASEGA | 31X73999 | USA | Taiwan | A-MD1UTVA6-2 | Headphone Out |
| Model 1 | HAA-2510 | VA6 | A10416197 | Japan | Japan | A-MD1JJVA6 | Headphone Out | |
| Model 2 | MK-1631 | VA1.8 | FJ8MD2SEGA | 151014280 | USA | China | A-MD2UCVA18 | AV Out |
| Nomad | MK-6100 | 50059282 | USA | Taiwan | A-NMUT-AV | AV Out | ||
| Nomad | MK-6100 | 50059282 | USA | Taiwan | A-NMUT | Headphone Out | ||
| CDX | MK-4121 | Y40 014198 | USA | Japan | A-CDXUJ-LO | Line Out | ||
| CDX | MK-4121 | Y40 014198 | USA | Japan | A-CDXUJ-HP | Headphone Out | ||
| CDX | MK-4121 | Y40 014198 | USA | Japan | A-CDXUJ-AV | AV Out | ||
| Sega CD | 1690 | A20113193 | USA | Japan | SCD | System | ||
It must be considered that this is a very small sample size, and no results or interpretations should be extrapolated as generalized conclusions about differences between models.
However, since several common trends are found and the systems were sourced from very different providers across a long period, it would be too much of a coincidence for these results to be by pure chance. I expect that we–as a community–can grow a bigger data set of recordings, in order to make better assessments in the future.3
The recordings presented in this chapters were made using the USB Lexicon Alpha audio card, due to the following reasons: it has a flat frequency response, it is available in the market at the time of writing, it works via USB and it is not expensive.4 The first system is the Reference, and the second one is the Comparison signal.
Even if the system volume settings won’t affect the analysis since normalization is performed in software,5 the volume control was set to its maximum when using the headphone out port. This was made in order to get consistent results, since variations could arise from the performance of the system amplifiers.
These models are an interesting starting point since the Reference system–the VA36 –is usually considered one of the best sounding versions of the system family line.7
On the other hand, the Japanese VA1 is the first revision to the launch JP VA0 system. This will give us an idea of how much the audio signatures changed from the launch units in Japan to the US VA3–which is also the first revision to the USA system, where the launch unit was the VA2.8
The resulting graph shows that the signals are quite similar, where only the higher frequencies–the treble–exhibit some deviation. The curve starts around 2kHz and slowly rises about 1dBFS above the 0dBFS line.
It is generally accepted that the minimum perceivable difference–under normal conditions–is around 3dB.9 So although a measurable difference exists–which is possibly noticeable under ideal listening conditions–the systems are very similar.
It is also noticeable that the percentage match bars are full, meaning that practically all the frequencies compared were matched.
Ever wondered if something was lost–besides stereo–when using the AV out port from the console instead of the headphone out? Figure 5.2 shows both ports compared using the same system.
Differences are present only in bass10 and treble11 . In the higher end of the spectrum, differences are less than 1dBFS and higher than 17kHz. The low end differences are more interesting–but still at a frequency range that would hardly matter for most setups, aside from the lost stereo. These reach a 3dBFS difference around 30Hz, so you get deeper bass when using the AV out if the music12 reaches those notes and your audio system has the means to reproduce it.
We’ll again be using the US VA3 as reference, now contrasted against a Japanese VA6. The VA6 is regarded as a good sounding unit in par with the VA3,13 and is also very common.
The curves closely follow the 0dBFS line, however the YM261214 amplitude is higher than the PSG amplitude by a really low margin, around 0.4dBFS. Although measurable, this would be even less noticeable than the difference against the VA1.
We’ll now compare two systems with the same VA6 motherboard revision. However, one is Japanese and the other is from North America. Results are displayed in Figure 5.4.
Once again, differences are minimal and quite similar to some previous results–in particular to the ones between the US VA3 and the JP VA1. But now FM seems to be closer and PSG is the one that is less than 1dBFS higher on the US system.
These are two other US VA6 systems, both made in Taiwan. And here are the results:
This is an interesting case since both consoles are the same motherboard revision and were manufactured in the same country.
Acoustically, these are very close matches with differences below 1dBFS. In this case FM is lower by that same amount and PSG matches the reference unit.
And now for something a bit more interesting. The same American VA3 unit we’ve compared to a few others, but contrasted against a Model 2 VA1.8. These Model 2 systems don’t use the YM2612, but a Yamaha YM3438 in an Application-specific integrated circuit (ASIC), which is a variation used for some later models.
These Model 2 versions–grouped with VA7 and other revisions–are regarded as having a lower quality sound output. This is due to various factors: the variation in FM synthesizer, the amplifier circuits used and the general audio circuit design.
The differences in this case are more noticeable: FM raises above 3dBFS, which is generally accepted as a discernible threshold,15 and does this around frequencies to which our hearing is quite sensitive,16 from 2kHz to around 8kHz.
But since a lot of data points are highly scattered, we can gather more accurate information for analysis using the Average Graph option as shown in Figure 5.7.
We can now appreciate that there are some relevant frequencies–that is, high amplitude in the reference signal–that pull the averaged graph lower between 200Hz and 3kHz-FM spectrum, and these go down up to 3dBFS.
We can also make out that peak in the human voice spectrum that goes 3dBFS higher, and then it dips in the treble above 6kHz to amplitudes lower by 6dBFS after 10kHz.
On the other hand, PSG seems quite similar aside from a bump around 60Hz and dipping in amplitude after 14kHz.
It must also be noted that, for the first time, there is a drop in the percentage of matched frequencies, shown in the bars detailed in Figure 5.8.
So far we had been getting results above 99.7%, and this time it dropped to 93.15% for FM.
The Sega Nomad is a portable version of the Sega Genesis, and it had only a single motherboard revision. Recordings were made via both: AV out and headphone out.
Our first contrast example will be using the headphone out port from both consoles, shown in Figure 5.9.
Some resemblance to the previous comparison to the Model 2 VA1.8 can be seen. In order to contrast both signals, an averaged graph is shown below.
The same general behavior from Figure 5.7 can be seen in FM, but PSG doesn’t fall in the same way in the high frequency range. This must be due to differences in the mixing circuit or amplifiers.
And if you’ve wondered about the difference between using the headphone out or the AV out in a Sega Nomad, here are the results:
In this case there are no differences above 100Hz. However the AV out has a more low frequency emphasis that is 3dBFS higher below 40Hz.
Due to the similarities shown between the Nomad and the Model 2 VA 1.8 when contrasted against the Model 1 VA3, here is the comparison between them using the AV out.
The consoles are indeed similar between themselves, with differences probably arising from amplification circuits. The Low pass filter is steeper in the Sega Nomad for FM, among other differences in the high rage regarding PSG.
Another interesting point is that both of these systems exhibit video refresh noise at a higher amplitude via the AV out than their Model 1 counterparts: around -45dBFS instead of -70dBFS.
The Sega CDX is an all-in-one system that includes the Sega CD unit. It has three different output options: headphone out, line out and AV out.
We’ll start by with the results of the Model 1 as reference contrasted to the CDX line out.
These are easily the most notorious differences between vintage retail hardware I’ve found so far.
The CDX PSG does not have the low pass filter present in Model 1 systems. The FM output is higher by at least 3dBFS, and it has a low pass filer around 9kHz.
Figure 5.14 shows the results when the average option is enabled.
This makes it easier to discern the curve that the FM audio follows when compared to the Model 1. It reaches as up to 9dBFS higher between the 4kHz-9kHz range.
We must remember that the Model 1, used here as reference, has it’s highest amplitude in the PSG signal with the current test. That’s why the results show FM higher instead of a lower PSG, since MDFourier does relative comparisons based on the Reference signal.
And for completeness, here is the differences graph when contrasting the Sega CDX line out vs the headphone out.
The headphone out has clear emphasis in the low frequency range, and even below 1.5kHz.
We are now comparing an extra line, Compact Disc Digital Audio (CDDA) from the Sega CD. It will be represented by an orange line in the graphs.
For our first case, we will compare if an American VA3 is any different from a Japanese VA6 when connected to the same Sega CD system.
The Japanese VA6 shows a lower amplitude for the CDDA audio in the final mix, at around a constant 1.5dBFS across the whole spectrum.
It is interesting to note that the differences in amplitude follow a very well defined pattern, as opposed to the fuzziness found when comparing FM audio. This demonstrates the natural harmonic variations an FM signal can present.
As a positive side effect from doing a precise frame alignment of the CDDA signals for the comparison process, the Analysis Software also displays the time it took the CD unit to start playing the audio track:
In this case the Sega CD took almost 9 frames to start playing the CD track from the moment the Basic Input/Output System (BIOS) was requested to do so. These results can be used to determine differences between drives–and could potentially tell us something about their maintenance status.
The difference in amplitude between regions is intriguing. It could of course be present just between these particular units. We’l explore it further in the following cases.
In Figure 5.17 we are contrasting the differences that arise when using the same US Sega CD unit connected to Japanese and American VA6 systems, both made in Japan.
It can be appreciated that the US VA6 unit shows a higher amplitude for the CDDA mix–at around 1.5dBFS–for the whole spectrum. This is the opposite from the previous case, but this time we are using the Japanese unit as reference.
This shows that the two American systems might precisely match in amplitude in all the compared signals.
Although I don’t have other Japanese systems to compare if the amplitude balance against CDDA is a regional difference, we can at least verify if American systems show the same balance. Figure 5.18 contrasts a VA3 and a VA6 both using the same Sega CD unit.
And yes, we do have a perfect match across the whole spectrum and for all the compared audio sources.
We are already familiar with the results of comparing a Model 1 VA3 and a Model 2 VA1.8 as shown in section 5.6. Here is the same comparison but with CDDA added to the mix:
It can be appreciated that the CDDA mix has a lower low pass filter in the Model 2 unit, starting at around 3kHz. For clarity, Figure 5.20 shows the results from the comparison just for CDDA.
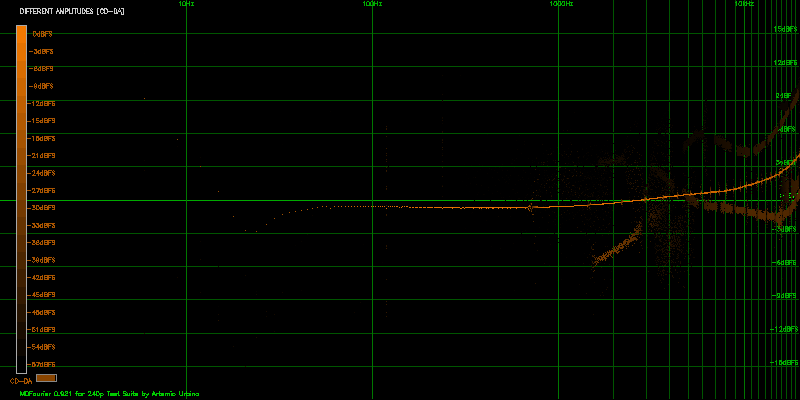
There are also other lines present in the results, which are probably the result of different harmonics that are created during the filtering and mixing process.
So far MDFourier has shown results that are consistent with previous empirical evaluations, and can support many such claims with data. I hope it can provide the community with a process that is repeatable and objective that can be used in any project where someone wants to preserve, compare, replicate or play with the results.
I believe these cases support the idea that this process has value, and that it can be replicated in as many platforms as possible. Audio has been historically relegated to a secondary position, when the audio visual experience is one–as a whole. Games are not the same without their acoustic experience.
This could help to document the original audio signatures of old systems. And of course, to enable the community to play with variations and modifications that are as valid as the ones the systems originally had at launch.
The project web page is available at http://junkerhq.net/MDFourier/, where the latest version of this document is available in PDF and HTML.
The Downloads page contains the following items:
The current version of the Analysis Software allows access to the main options of MDFourier. It is a Windows executable and all corresponding files must be placed in the same folder. Uncompressing the package should have all that is necessary to run the program.
After executing MDFourierGUI.exe you should be presented with the following interface:
In order to generate the output graphs, two files must be selected to compare them. One as a Reference and the other as the Comparison file, as detailed in section 3.
The following sequence of steps indicates the typical work flow within the GUI:
The Analysis Software will display the output text from the command line tool, including any errors or progress as it becomes available.
Keep in mind that the Open Results button will only be enabled after a successful comparison between files has finished, and it won’t open a second instance of the window if you have one already present.
The default options will generate graphs that work on most situations. In some cases fine tuning the results might highlight specific aspects. These options will be described in the following sections.
The currently available options in the Analysis Software are:
In order to reduce spectral leakage1 when applying the DFT, a filtering window2 is applied to each element to be compared between both signals. Since we are producing the sound ourselves from the Tone Generator, the signal can be analyzed as periodic,3 and has a natural attack and decay rate if possible.
By default we use a custom Tukey window with very steep slopes.4 MDFourier does offer alternate windows as options for further analysis.
Each dot in the Differences graph uses the X axis for the frequency range and the Y axis for the amplitude difference between the Comparison and Reference signals.5
Color intensity of each dot is used to represent the amplitude for that frequency in the Reference signal. In other words, how relevant it was to create the original signal in that note. Please refer to chapter 4 in order to see examples of their use.
A color scale is presented in each graph, with the color graduation and the corresponding amplitude level.
The options are useful to highlight or attenuate these differences by applying the range to one of the following functions.
They are sorted in descending order. The topmost option will highlight all differences; and the bottom one will attenuate most of them, and show just the ones with highest amplitudes in the Reference signal.
All filters, their graphs and effects are listed in appendix L.
When designing the audio test signal for use during analysis, one consideration is how to balance gathering more information versus the length of each recorded audio signal.
Having a short audio test signal is desirable for several reasons: it reduces the time taken to record from each system, minimizes the storage space required for archival, the analysis software is much faster with shorter archives, and it also makes distributing the audio recordings easier, due to a smaller resulting file size.
In contrast, when applying the Fourier transform a compromise is made between frequency detail and time accuracy, very similar to the Heisenberg’s uncertainty principle. If we compare a longer signal for each element, we end up with more frequency information. In our case, we don’t care much about time accuracy but we do care about the length of the test. Nobody wants to record a 5 or 10 minute signal for each test to be made.
The compromise made is to use sub second signals for each element to be compared. Since the time and sample rate determine how the DFT frequency bins6 are spaced after analysis–and how much information we end up analyzing–the end result is a lower graph resolution.
Zero padding the input signal for Fourier analysis is a controversial subject7 , but for the present application no adverse effects have been found. This might be the case since we control how the source signal is generated, with a predetermined attack and decay. However, it is disabled by default so the results presented can be free from questioning regarding the effects, and available for cases where more precise frequency information is needed with no spectral leakage to adjacent frequency bins.
Several graphs will be generated as a result of the analysis. There will be several graphs of each type in the output folder8 . One for each type, and one that summarizes all types in a single graph.
All graphs are saved in the PNG9 format, which is lossless and open source. Please read section 4 for examples and a guide to interpret their meaning.
Enabling this option creates the most relevant output graphs from MDFouriuer. These contain the amplitude difference for the frequencies common to both files across the hearing spectrum using the Reference file as control.
If the files are identical, the graph will be a perfect line across the 0dBFS line. In case the signals differ, a scatter graph will show how it behaves across the typical human hearing spectrum.10
The file names for these graphs have the format:
DA_Reference_vs_Comparison_block_options.png
Graphs the frequencies available in the Reference file but not found in the Comparison file within the significant amplitude range. This is in effect a Spectrogram, but limited to the frequencies that were expected to be in the intersection but that were not present in the Comparison file.
The file names for these graphs have the format:
MIS_Reference_vs_Comparison_block_options.png
This option traces an average line on top of the Difference graphs, making it easier to follow the trend when the output has severely scattered data. It is off by default.
The curve is created by averaging time segments from the frequency data sorted in ascending order. A Simple Moving Average11 is then calculated to smooth out the results.
The curve is weighted according to the Color Filter Functions described in section B.1.2, by repeating each data point by the amount mapped in the 0-1 interval described by the function.
As a result, the average will follow the relative amplitudes from the Reference signal proportional to the selected filter function.
If there is need for a graph without weighting, please disable the Color Filter function.
The file names for these graphs have the format:
DA_AVG_Reference_vs_Comparison_block_options.png
This option will generate three graphs, one noise floor spectrogram for each file and a comparison graph. Both are plotted with the same scale, so they make sense when compared.
The file names for these graphs have the format:
NF_Reference_vs_Comparison_block_options.png
Plots all the frequencies available in each file.12 Two sets of spectrograms are generated, one for the Reference file and one for the Comparison file.
The file names for these graphs have the format:
SP_AVG_Reference_vs_Comparison_block_options.png
This checkbox enables the text field to send any extra commands that are not available via the GUI to MDFourier.
Current options as of version 0.954 are:
Sending -h in this field will enlist all the currently supported options for your version.
A log is always created by default when using the Font End, however this option enables a verbose version with the whole frequency analysis and many other details dumped to the file.
Useful for reporting errors or unexpected behavior. Please send the audio files if possible as well!13
All these parameters are defined in the mfn configuration files inside the profiles folder.1 . Here is the profile used to compare PC Engine/Turbo Grafx-16 audio characteristics:
This file defines what MDFourier must do and how to interpret the WAV files. For now it can read 44.1kHz and 48kHz files, in Stereo PCM format.
The first line is just a header, so that the program knows it is a valid file and in the current format.
The second line is the name of the current configuration, since I plan to add support for different consoles or arcade hardware in the future. This would imply creating a new mfn file for each configuration, and a specific Tone Generator to be run on the hardware.
The third and fourth lines are the expected frame durations in milliseconds for NTSC and PAL respectively.2 This is only used as a reference to estimate the placement for the blocks within the file before calculating the precise frame rate of the recording as captured by the sound card. After that is calculated, each signal uses its own timing in order to be fully aligned. Frame rate variations in the order of 0.001ms are natural, since we have an error of 1 ∕ 4 of a millisecond3 during alignment, and differences also occur by the deviations in sample rates and audio card limitations4 .
The extra parameters in the NTSC and PAL lines define the characteristics of the pulse tone used to identify the starting and end points of the signal within the WAV file. Its frequency, relative amplitude difference to the background noise (silence), and length intervals that will be better explained in future revisions of this document.
The fifth line defines how many different blocks are to be identified within the files. There are six blocks in this case.
Each block is composed of six characteristics: A Name, a type, the total number of elements that compose it, the duration for each element specified in frames, the color5 to be used for identifying it when plotting the results and a letter marking if it is a stereo or mono element.6 Each block must correspond to a line with these parameters.
For example, FM audio has been named "FM", type 1, 96 elements of 20 frames each and will be colored in green. Definition is in frames since emulators and FPGA implementations tend to run at different frame rates than the vintage retail platform, which result in different durations. The only way to align them, is by respecting the driving force that tied this up in the old days: the video signal.
There are currently two special types, identified by the letters ’s’ and ’n’. The first one defines a sync pulse, which is used to automatically recognize the starting and ending points of the signal inside the WAV file.
The second one is for null audio, or silence. This silence is used to measure the background noise7 as recorded by the audio card.
MDWave is a companion tool to MDFourier. During development and while learning about DSP, I needed to check what I was doing in a more tangible way. So, in order to visualize the files in an audio editor and listen to the results MDWave was born.
It takes a single WAV file as argument, and loads all the parameters defined in the configuration file in order to verify the same environment.1 To run it, simply press the button next to the selected profile.
The output is stored under the folder MDWave, and a subfolder with the name of the input audio file. The default output is a WAV file named Used which has the reconstructed signal from the original file after removing all frequencies that were discarded by the parameters used.
This means that it does a Fourier Transform, applies the selected window2 and estimates the noise floor. The highest amplitude frequencies are identified and limited by range for each element defined in the configuration file, and the rest are discarded. An Inverse Fourier Transform is applied in order to reconstruct the WAV file and the results are saved.
The opposite can be done as well by specifying the -x option, and the result is a Discarded WAV file, that has all the audio information that was deemed irrelevant and discarded by the specified options. With this you can listen to the produced files and determine if a more thorough comparison is needed.
In addition, the -c option creates a WAV file with the chunk that corresponds to each element from the Reference file being used, trimmed using the detected frame rate. Two chunks are created for each element, the Source WAV chunk has the element trimmed without modification and the Processed WAV chunk has the same element but with the windows and frequency trimming applied.
It has a few more command line options, which I’ll detail in later revisions of the document. You can type mdwave -h in your mdfourier folder for details.
Since each signal is probably at its own distinct amplitude, we need to perform a normalization process in order to have a common comparison point between them.
Each type of normalization has its own strengths and weaknesses, but the frequency domain normalization designed for this process is always accurate with respect to the Reference signal, but might be confusing in some corner cases1 if the underlying causes are not well understood when interpreting the results.
Since silence can’t be used as reference2 , the only other option is fixing points from within the signal. Every normalization process used follows a different logic for fixing one such point for comparison.
The default is to do this in the frequency domain3 , but there are two other options available via command line4 . All three methods are described in the following sections.
This is the default option used by the software. It involves finding the highest magnitude5 from the Fourier Transform of the Reference signal before amplitudes are calculated. Then a corresponding match in the Comparison signal’s frequency spectrum for the same block is searched for.
This means that the exact same fundamental frequency with the highest magnitude value is searched for, occurring at the same position in time–which corresponds to the block. Having both points, a meaningful reference point is set for the comparison, and the relative amplitudes between the signals can be calculated.
In order to calculate the amplitudes, 0dBFS is matched against the absolute highest magnitude from the Comparison file6 , after both signals have been relatively normalized in amplitude against the reference point.
This method has shown to be always accurate within the tests. However, results can be unexpected in certain corner cases as the one shown in appendix I.
The process is very similar to the frequency domain variant but it is done using the raw audio samples directly from the WAV file.7
The highest amplitude is searched for within the samples of the meaningful audio signal, as dictated by the configuration file.8 The corresponding segment in time is then located in the Comparison file, and a pre-defined duration is searched for the sample with the maximum local value.9
The Comparison signal is then absolutely normalized to 0dBFS,10 and the Reference signal is then relatively normalized using the adjusted local maximum value. This follows the same rationale described for the frequency domain equivalent.
Although the results can sometimes be deceivingly familiar, they are not correctly referenced in corner cases,11 and they do not represent the real relation between the signals. However, they can be useful for analysis while in the process of understanding how to interpret the graphs.
This normalization option also takes place in the frequency domain. The idea is to average the highest magnitudes–the fundamentals–from all segments and use the resulting ratio calculated between both signals to normalize them.
The results are always centered around the 0dBFS line in the Differences graph, allowing a globalized view. However, the amplitude differences are not to be relied upon for calibration, since they are not relative to a fixed point from the Reference signal. This option is just available for cases when both signals present a high difference rate between them, which is unexpected but possible.
The frame rate is the amount of frames per second a system sends to the display. Since the Tone Generator runs from within the target system, we are subject to the internal timing. Every time a frame starts the process for being sent to the display, an event called vertical sync occurs. This is the driving clock for the whole console.1
It is vital for the process to have a basic unit of time, in order to segment the file in the chunks needed for analysis and to send the correct values to the Discrete Fourier Transform.
Signals generated from different sources can have dissimilar frame rates, even when running the same programs and representing the same platform. This can be due to several reasons: having a different display technology as target, hardware inconsistencies between revisions, etc.
Another source for variation is the audio capture device, since these can vary slightly in their sample rate clocks. But usually these are lower variations that are reported and compensated for internally. It has also been found that some audio cards use a more inaccurate clock when sampling at 44.1kHz and a very accurate one when using 48kHz.2
The frame duration is the basic unit of measurement, since we are dealing with signals that are well below one second. Because of this, the configuration file3 defines the expected frame duration in milliseconds as measured from a vintage console. One such example is the frame duration as measured from an NTSC Sega Genesis using an oscilloscope.4 as shown in Figure F.1
The oscilloscope shows a frame duration of 16.88ms, and this is the value used in the configuration file5 for the initial frame rate calculations.
After the sync pulses are detected,6 a new frame rate value is calculated from the audio file. This new frame rate is used across the whole process, and can vary from the vintage console due to a combination of different reasons.
Every audio card can have a slightly different sample clock,7 and this variation will affect the starting and ending points within the recording. Such variation can be detected and estimated from the audio signal, and it is reported if the verbose log8 option is enabled.
The selected sample rate for recording can also affect the sample clock precision even while using the same card.9
The most important case, and the one for which the sync pulse solution was implemented, is when comparing a modern system such as an emulator or a FPGA implementation. These usually run at modern refresh rate10 for better compatibility with current display technology, such as HDTVs, since the vintage hardware has refresh rates that are slightly off-spec.11
Since frame rates differ and the system uses the frame rate as a master clock for program execution, the resulting audio recordings also have a difference in length. For example when using an implementation adjusted for NTSC, there is a 0.001 second difference in each block of 20 frames. Although this seems to be negligible, it adds. In a one minute recording, such as the ones used for MDFourier, every note was misaligned due to this difference.
The software discards the extra duration in these cases, adjusting for fractions of a second every time they reach the next sample. Since the notes are not played during the whole 20 frames and the window filters help to compensate the signals, the comparison is perfectly aligned for the tests. The reader can verify these results via the MDWave tool.12
Sometimes the audio recording has different amplitude levels between the right and left audio channels, this is referred to as stereo imbalance. Whenever possible, MDFourier detects and auto compensates this imbalance in order to give a more uniform graph result. The default behavior can be disabled if desired with option -B.1
This should only be a concern if an imbalance in the source system is suspected.
Two causes for imbalance have been identified. At the time of analysis MDFourier cannot possibly discern between them, and both can be present at the same time.
It must be noted that the internal PCI audio card used during testing has minimal audio imbalance–0.0018% on average–and this allows detecting system amplification deficiencies with consistency.2
The sound card balance issue can be minimized by adjusting the knobs carefully. MDFourier can be useful for compensating this via repeated testing, since any imbalance is reported in the output. It has also been found that leaving gain at zero in some cards, like the M-Track, produces more pronounced imbalance than at 50%. However this requires recording from a source that is known to be balanced.
In order to detect and compensate audio imbalance, at least one monaural block must exist within the mfn3 configuration profile being used.
The software assumes that the monaural signal must be the exact same amplitude between left and right audio channels, and compensates by normalizing the samples from one unbalanced channel by adjusting them via the proportional ratio.
During the initial development of the software there was a single instance where unexpected variations were present between different recordings of the same hardware using the same audio capture card as shown in Figure H.1.
After analysis, it was found that the difference was present only in the left channel and was caused by a severe difference in temperature while recording. The room was at 29∘C1 as shown in Figure H.2, and the Sega Genesis Model 1 VA3 under testing had been powered on for around 30 minutes.
At first, warm up differences were suspected. But after some cooling, cold boot2 and measurements using a thermal camera it was determined that the room temperature on top of the warm up was the culprit, since the results could not be replicated when the room had cooled down to 22∘C3 .
In order to replicate the results, its vents were obstructed to prevent heat dissipation4 for a brief period. The results could be replicated at will under these conditions after just a few minutes of use.
It must be noted that the temperature of the headphone amplifier5 of the console reaches 82.9∘C6 with cover removed as shown in Figure H.3, so higher temperatures are expected with it closed. This is important since some of the stock capacitors around the headphone amplifier are radiated due to proximity, and can probably reach temperatures beyond their intended rating in warm climates.
While testing the default frequency domain normalization,1 I found that one artificially generated case would produce results that were unexpected and surprising. After analysis, I believe them to be the correct handling of the data, and the appropriate comparison results.
For this example we’ll modify a file as detailed in Scenario 3,2 but this time a 1zkHz 6dBFS tone will be added instead of the 500Hz from that previous case.
I was expecting the result detailed in Scenario 3, but was greeted with the graph shown in Figure I.1:
I thought it was a bug in the processing of frequency domain normalization. But after careful analysis, this is the correct result from such process.
It is all due to a big coincidence: the maximum global amplitude of the original signal used for this scenario is located at 1005.99Hz, at just 5.99Hz from the 1kHz peak that was artificially inserted. As you might sharply point out, Figure I.1 doesn’t show the peak 6dBFS below zero. But that is because it is not centered at 1005.99Hz.
Here is the result when centering the peak at 1005.99Hz:
Now the majority of the curve is 6dBFS below zero, and the peak is at zero. But why?
As explained in appendix E, the process of frequency normalization consists in finding the highest amplitude in the signal and use that as a reference point for matching both signals. In this case, both signals have their maximum at 1005.99Hz, but we also modified the comparison file to have a 6dBFS 1005.99Hz peak. As a result when using the original reference file as a model and judging the comparison file against it, the rest of the signal has been lowered from this perspective.
This would mean that if two systems had these audio signatures, the resulting graph would tell us that the comparison console is–in general–producing the frequencies at lower amplitudes. If the comparison system had to be modified to match the reference system, the rest of the frequencies in the signal should be raised by 6dBFS, since the single point at 1005.99Hz already matches the reference signal. It is just a matter of perspective. It helps keeping in mind that MDFourier does relative comparisons, and in this framework the reference file is the absolute model.
In case we’d like to see a graph that would probably be easier to understand–but which I now believe is not as accurate in representing the relative differences–one could enable the time domain normalization. The output graph would be the by now familiar result from Figure I.3:
This graph tells us the exact same thing: if the comparison signal is to be modified to match the reference signal, the peak at 1005.99Hz must be lowered by 6dBFS. Since the results in both cases would be the same, both interpretations are equivalent.
However, I am inclined to adopt the first position, since it has an absolute reference point. Whereas the second graph and interpretation must be modified depending on the input. For this second scenario to work, our framework needs to be modified for special cases–that are highly unlikely to be found in the wild. And since that creates unnecessary inconsistencies and results in imprecision, the time domain normalization is not used by default.
I’m positive several deficiencies in my implementation still elude me. However here are a few I’m aware of and have not addressed yet.
Please contact me if you are aware of any details that I have missed.1
This appendix lists the equation and curve of each Window Function used to limit spectral leakage as described in section B.1.1.
The default is a Tukey window selected for this purpose. It uses α = 0.6, zeroing just a few samples, with minimal spectral leakage and good amplitude response.
The following equation is used to create the slopes:
 | (K.1) |
And this is the resulting graph of the Tukey window, ranges are 0.0 to 1.0 horizontally and -0.1 to 1.1 vertically.
Detailed information can be found in the reference webpage [25].
When selected, a typical Hann window is used. This should be used to get the last spectral leakage, with a very small trade off in amplitude accuracy.
![hann[x] = 1(1- cos(2π(x+-1)))
2 n+ 1](mdfourier1x.png) | (K.2) |
A typical Flat top window is used, selecting this will target amplitude accuracy against frequency bin precision.
flattop(x) = 0.21557895 - 0.41663158cos(2π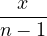 ) + 0.277263158cos(4π ) + 0.277263158cos(4π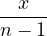 ) ) | ||
- 0.083578947cos(6π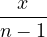 ) + 0.006947368cos(8π ) + 0.006947368cos(8π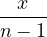 ) ) |
A typical Hamming window is used, presented for completeness and reference since the samples are never zeroed out.
![hamming [x] = 0.54 - 0.46cos( 2πx-)
n- 1](mdfourier6x.png) | (K.3) |
When this option is selected, no filtering window is applied to the signal before applying the DFT, which is equivalent to a rectangular window. Since the signal is unprocessed, any uncontrolled decay or even the noise floor can be factored in as part of the signal.
There is more information on windows and their usage in the reference webpage linked from [14].
This appendix contains a description, graph and example of each Color Filter Function from section B.1.2.
No filtering is applied, as a result all differences are plotted using the brightest color.
A square root function will only attenuate the lowest amplitude differences. This
applies the formula  to the amplitude from the reference signal, in order to
assign the brightness.
to the amplitude from the reference signal, in order to
assign the brightness.
A Beta Function filter with parameters β(3,3) will attenuate a bit more from the lower range, still showing most of the differences.
The linear function is the default selection, and has no bias. Half the dynamic range corresponds to half the color rage.
A squared function dBFS2 will attenuate a lot more differences. As a result, only the frequencies with the highest amplitudes from the reference signal will be brighter.
A Beta Function filter with parameters β(16,2) will attenuate almost all the differences, and only the frequencies with the highest amplitude in the reference signal will be brighter.
For capturing the audio files, an audio capture device is needed. It is recommended to use a musical grade audio card in order to get a flat frequency response across the human hearing spectrum. Fortunately, these devices have become more affordable.
So far four audio cards have been used in my personal setup. The sample recordings available for download1 were made with three cards of them, a complete set with each one of them.
I have no association or business relationship with these products, they are just presented as working examples. As more people use the software and we–as a community–compare files, this list can be expanded with recommendations.
Some cards marketed for podcasting and audio cassette digitization were tested,6 but they didn’t show a flat frequency response. You should try to use a sound card that is aimed to musicians or instrument recording.
Sound cards have their own internal clock for sampling,7 which can sometimes deviate enough so that MDFourier can report frame rate differences. From my tests, this is more prominent when using the 44.1kHz sample rate, and minimized when using 48kHz. The effect is compensated for while loading the file and during trimming, so it shouldn’t be a problem due to the small variations this produces in the frequency domain.
Any computer and operation system can be used if you are compiling the source code from scratch,8 but a statically linked Microsoft Windows executable is provided for convenience, alongside a front end. See chapter B for instructions on using the GUI.
You’ll need either the provided example audio files9 or to create your own, by recording from your own source. This is probably the desired route, since you will want to compare against your files.
The console needs to run the Tone Generator created for that platform–which are provided with the rest of MDFourier. If possible this will be integrated into each version of the 240 test suite [6].
In order to run these, you’ll either need a flash cart or a custom loading solution compatible with the target platform.
You’ll need cables–and maybe some adapters–to connect the audio output from the console to the input of your audio capture card.
Your audio capture card will probably be bundled with some audio editing software, or you can use Audacity [29] or Goldwave [30] depending on your operating system.
MDFourier needs a few libraries to be compiled. In Linux, UN*X based systems and Cygwin [24]; you can link it against the latest versions of the libraries.
The following implementations are also used and included with the source files:
The pre-compiled executable of the Analysis Software for Windows is created with MinGW [23], and statically linked for distribution against these libraries:
The makefiles to compile either version are provided with the source code [5].
This is the list of colors that can be used in the MFN configuration file described in appendix C:
MDFourier Copyright (C)2019 Artemio Urbina
This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with this program. If not, see https://www.gnu.org/licenses/.
You can contact me via twitter http://twitter.com/Artemio or e-mail me at aurbina@junkerhq.net.
I’d like to thank the following people for helping me so this software and the present documentation could be completed.
First and foremost to Michelle, you helped me find the time to learn, code, experiment and write for this project. It would have been impossible without your support, thank you.
To Ricardo Pestaņa (Rhe7oRPG) for guiding me through the unfamiliar process of giving shape and sense to this text. I am not good at writing, and this would not be close to its current form without your feedback, time and input.
Fernando Villaseņor for your patience and attention when discussing the ideas while I was shaping this project. Your comments gave me confidence that I could transmit the ideas I wanted to with some clarity, and pushed me forward in order to complete and publish the project.
Tianfeng for assisting me by proofreading the text and helping to make it readable. Having a native speaker check the documentation greatly reduced the awkwardness of my style, and helped the text flow better. Most importantly, thanks for taking the time and resources to create your own audio recordings, and to compare results when the project needed it.
Bernard Bygott for his enthusiasm, ability, critical analysis and bug finding skills. Your help has been crucial for this project. The time and resources you’ve poured to make this a better solution have been a driving force while improving MDFourier.
Robert Neal for your ability to create communities and your disposition to help others. The value of being able to reach out for feedback cannot be appreciated enough.
Marc "Try4ce" Duddleson and Coury Carlson from "My Life in Gaming", who indirectly seeded this project while they worked on a script. The feedback loop we’ve created helped me bounce ideas with you from time to time. Marc’s feedback while proofreading allowed me to remove unnecessary complexity from the text, and your input made me notice the need of what became the Audio Basics chapter.
Enforcer for detecting a bug in the audio routines of the 240p Test Suite, and making sure I didn’t carry that on to the MDFourier test program. Thanks for reaching out.
To Oscar Toledo G. (Nanochess) for proofreading the document and pointing out some quirks about my writing style. This helped to improve the flow of the text.
Mauricio Lechuga, thank you for your time and attention to the project. our feedback helped me push in the right direction to create the current version of this document.
Aldo Martinez for listening and showing interest in the project. Talking about teh ideas helps to shape them out clearly.
John Linneman thank you for detecting a bug in my audio program for the system and for using the early versions of the software for comparisons.
To Rolando Cedillo for listening to my thoughts and for letting me borrow an audio card for testing. This helped me shape the results and confirm some facts that were very important for the validity of my results.
M.I.J.E.T. as always thanks for your well thoughts comments and ideas, they helped me to add a bit more rigor to my methods and process.
Byuu thanks for reading and believing in the possibilities this project may offer.
Special thanks to Soltan_G42 and Rysha for your enthusiasm and feedback, it was very encouraging at a time the project was shaping out.
And thanks to Psikyo, since repairing and playing their Strikes 1945 PCB helped me think about solutions and to clear my mind between coding and writing sessions.
[1] Bracewell, Ronald N. The Fourier Transform and Its Applications (2 ed.). McGraw-Hill. ISBN 978-0-07303938-1.
[2] Ace, GUIDE: A complete overview of the many Sega Genesis/MegaDrive models, Sega-16, http://www.sega-16.com/forum/showthread.php?7796-GUIDE-Telling-apart-good-Genesis-1s-and-Genesis-2s-from-bad-ones
[3] The Best Version of the Genesis, RetroRGB https://www.retrorgb.com/genesisversions.html
[4] Sega Mega Drive/Hardware revisions, Sega Retro, https://segaretro.org/Sega_Mega_Drive/Hardware_revisions
[5] Github, MDFourier source code C99, https://github.com/ArtemioUrbina/MDFourier/.
[6] 240p test Suite, Wiki web page, http://junkerhq.net/240p/.
[7] Fastest Fourier Transform in the West., web page, http://fftw.org/.
[8] libPNG, web page, https://libpng.sourceforge.io/
[9] libFLAC, web page, https://xiph.org/flac/
[10] GNU Plot Utils, web page, https://www.gnu.org/software/plotutils/
[11] An implementation of a ton of sorting algorithms in C with a user-defined type, web page, https://github.com/swenson/sort/
[12] Human Hearing: Amplitude Sensitivity, Mark Sanfilipo — April 04, 2005, https://www.audioholics.com/room-acoustics/human-hearing-amplitude-sensitivity-part-1
[13] incbeta, Incomplete Beta Function in C, https://codeplea.com/incomplete-beta-function-c/.
[14] Window Types: Hanning, Flattop, Uniform, Tukey, and Exponential , web page, https://community.plm.automation.siemens.com/t5/Testing-Knowledge-Base/Window-Types-Hanning-Flattop-Uniform-Tukey-and-Exponential/ta-p/445063/.
[15] dB Full Scale, https://www.sweetwater.com/insync/dbfs/
[16] Sound Card Sampling clock variation http://www.stu2.net/wiki/index.php/Calibrate_Sound_Card/
[17] So how accurate is a typical PC sound card? How stable is the output? How would one measure this? Experiments with a PC sound card by leapsecond http://www.leapsecond.com/pages/sound-1pps/
[18] Each sound card has it’s own sampling clock, Goldwave support forums http://www.goldwave.ca/forums/viewtopic.php?p=17470
[19] D/A and A/D | Digital Show and Tell (Monty Montgomery @ xiph.org) https://www.youtube.com/watch?v=cIQ9IXSUzuM
[20] Harris, Fredric j. (Jan 1978). "On the use of Windows for Harmonic Analysis with the Discrete Fourier Transform". Proceedings of the IEEE. 66 (1): 51–83. https://web.mit.edu/xiphmont/Public/windows.pdf
[21] Spectral Leakage and Zero-Padding of the Discrete Fourier Transform https://dspillustrations.com/pages/posts/misc/spectral-leakage-zero-padding-and-frequency-resolution.html
[22] Why is it a bad idea to filter by zeroing out FFT bins? https://dsp.stackexchange.com/questions/6220/why-is-it-a-bad-idea-to-filter-by-zeroing-out-fft-bins
[23] MinGW, Minimalist GNU for Windows, http://mingw.org/.
[24] Cygwin, a large collection of GNU and Open Source tools which provide functionality similar to a Linux distribution on Windows. https://www.cygwin.com/
[25] Tukey window, Recording Blogs https://www.recordingblogs.com/wiki/tukey-window
[26] M-Audio Audiophile 192, Specifications, https://www.soundonsound.com/reviews/m-audio-audiophile-192/.
[27] Lexicon Alpha USB card, Product web page, https://lexiconpro.com/en/products/alpha/.
[28] M-Audio M-Track USB card, Product web page, https://www.m-audio.com/products/view/m-track.
[29] Audacity web page, https://www.audacityteam.org/.
[30] Goldwave product web page, https://www.goldwave.com/.
[31] Adam Hayes, Simple Moving Average - SMA Definition https://www.investopedia.com/terms/s/sma.asp
[32] Human Speech Spectrum, Frequency Range, Formants, web site, http://www.bnoack.com/index.html?http&&&www.bnoack.com/audio/speech-level.html.
[33] Noise Level Chart, web site, https://www.noisehelp.com/noise-level-chart.html
[34] Audio Spectrum Explained web site, https://www.teachmeaudio.com/mixing/techniques/audio-spectrum/.